Quad Tree

Since the dawn of the first video game, collision has always been a part of any game created. Lots of collision algorithms are out there, some are easy to master and some are not. However, any collision system implemented must have some way to check if the interaction between two objects actually occurs. Checking for collisions between a few objects in a scene is relatively easy. Altough, when it comes to checking for collision between hundreds, or even thousands of objects using the dreaded pairwise comparison, that will take a great toll on performance. Luckily, there exists many collision checks that offer efficiency and speed. One of which is the quad tree data structure.

A quad tree is a tree data structure used in spatial partitioning, so that it's easy to traverse and search. You may be wondering what exactly is spatial partitioning? To put it in simple terms, spatial partitioning is the process of subdiving a scene into multiple regions, and that is exactly what a quad tree does. It recursivly subdivids a game's world into smaller and smaller sections. Generally, a quad tree must fulfill a certain criteria where each non-leaf node must have four children, every leaf node has a maximum number of objects and if that number is exceeded the node is split.

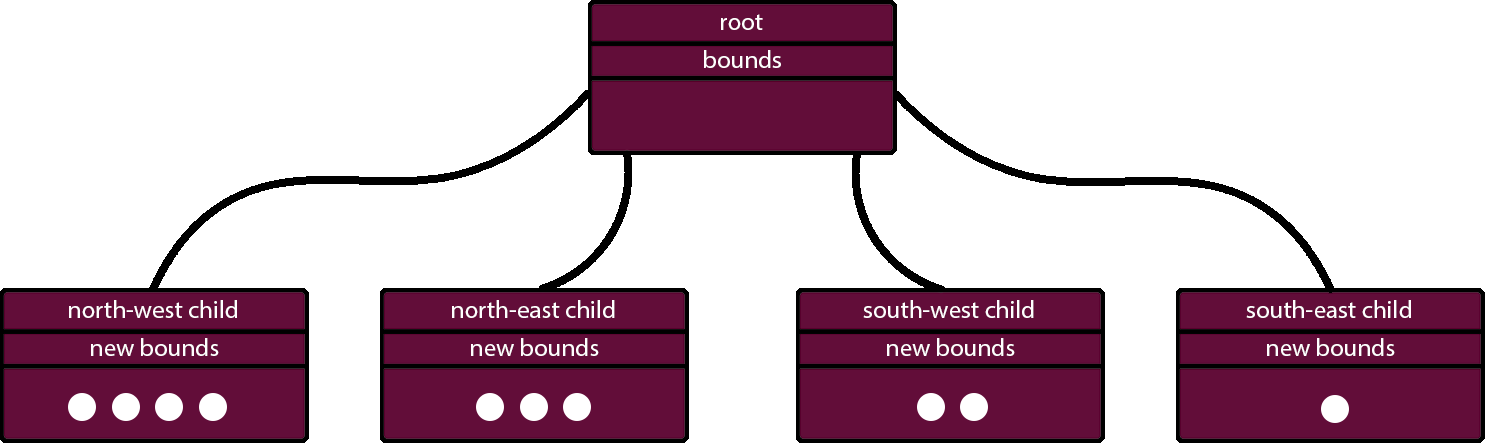
An important point to keep track of is that the leaf nodes only store data, while the parent nodes store info on how to get to their children. As seen in the above diagram, the root node reached the maximum number of objects allowed to be stored therefore it has split creating four children each holding the objects according to their postion in the world.

As mentioned above, the whole purpose of a quad tree is to subdivide the world and arrange objects in that world in various nodes. But why do we subdivide exactly and how is it done? The whole premise of subdivision is to group objects that are close to each other and have a high possibility to collide with one another. This ultimately reduces the number of checks needed and in return boosts performance. Any quad tree starts with a root node holding the scene boundry and all the objects inside that scene, once the number of objects exceed the node's limit the boundry is divided into quadrants. Each quadrant is held by it's respective node and all objects that where held by the parent node in our case the root will be checked by each child node if they are within their boundries or not, if true then they're transfered if false the other nodes will be checked.

Press the left mouse button to draw a point in the scene below or the right mouse button to remove a point from the tree, and adjust the slider to configure the maximum number of points a single node can hold. Press the reset button if you want to start over.

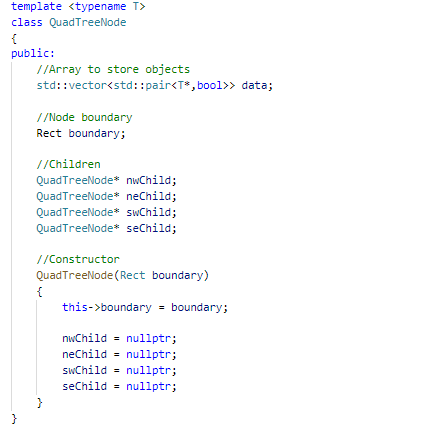
So, how do we implement this? To build a quad tree we first need to create a root node. A quad tree node consists of an array that stores the objects, a pointer to it's four children and it's boundary. It's only a few lines in C++.

Now that the node class is done, we need to actually start implementing the quad tree itself. A quad tree has three important functions. Insert, update, and query. We'll start by creating core functions for the quad tree and then we'll get into the more important functions.

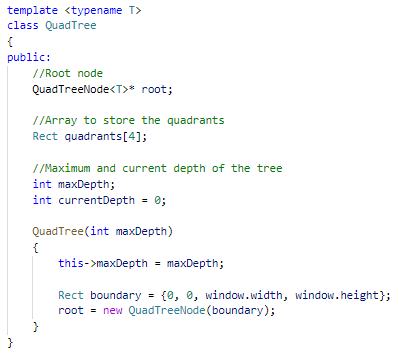
First, we'll create a quad tree class that holds a root node, the current and maximum depth to prevent the tree from infinitly recursing if objects are too close to each other and an array to hold the smallest quadrants. Now onto the functions.

IsLeaf and InBoundary are two important functions that will be used in the insert function. They're pretty much self explanatory. The first function checks if the node passed is a leaf or not by checking its children, and the second function checks if the object's position is within the node's boundary.

Inserting and removing objects in and out of a quad tree is fairly simple. As discussed earlier non leaf nodes can not store objects they only store data on how to get their children, also we have to keep in mind that once a node reaches it's maximum number of objects held it should subdivide. So, let's see how to implement this.

The insert function requires a split function to be called once the maximum is reached. Essentially, what happens here is we take the minimum and maximum points of the boundary (A minimum point of a rectangle is the top left point and the maximum point is the bottom right point), afterwards we divide the max points which are in reality the width and height by two to get equal quadrants and store them in the quadrants array. Just like that we have equal quadrants that are ready to be stored in their respective nodes. Finally, we need to implement the insert function.

If you haven't noticed already we're using BFS (Breadth first search) to traverse the tree and insert an object in it's appropriate node. We start by declaring a queue, then enqueuing the root node to that queue. Afterwards, we dequeue the node inline and check if the object we passed is a leaf, is within it's boundary and has capacity to store one more object if all these conditions are valid then we can insert. However, if all conditions satisfy our statment but the object is not within the node's boundary then we grab another node from the queue. As you guessed it, if the node is not a leaf then we enqueue all it's children. Now, comes the tricky part. What if the node is a leaf and the object is within it's boundary but maximum capacity has been reached? This is when we call the split function and recursivly call the Insert function to insert all the current node's elements into it's children. Keep in mind, before we split we need to check if the maximum depth has been reached. If so we simply return, that way we ensure that the tree can no longer subdivide itself. Now let's see how to implement the remove function.

Removal in a quad tree is pretty straight-forward, just like in insertion we traverse the tree using BFS then and check if the node is a leaf or not. If false we enqueue it's children, if true we iterate through the objects stored inside the node and delete the target object. However, if you look closely we have a Shake function being called with a parent node passed as a parameter. Let's disect this function.

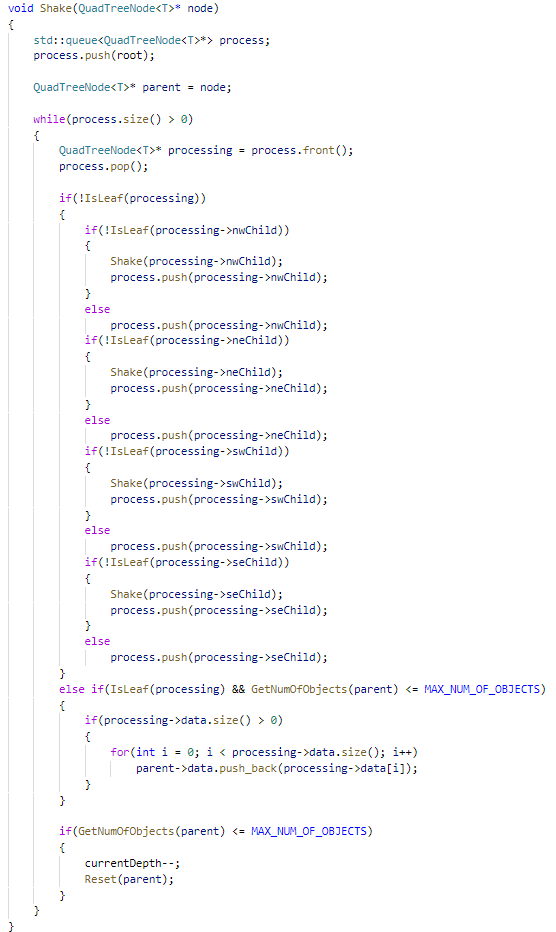
As the name says, the shake function shakes the tree forcing it to drop it's empty leaves that are unnecessary to be present. This means if the total number of objects within a node's children is less than the maximum number of objects permitted per node the current child nodes are eliminated, and the node becomes a leaf. And that's exactly what the above function does, we pass in the parent node where an object was removed from one of it's children. Afterwards we obtain the total number of objects below that parent and if their count is less than the maximum allowed we transfer all objects contained inside the children node to the parent node, decrement the current depth and Reset (Delete the children and assign the parent's child pointers to null).

Now that we have all the core functionalities set up it's time to actually make the quad tree do what it's supposed to do and that is improve performance when it comes to collision checks. Before we jump into the code let's see how a quad tree signficantly optimizes performance.

In the scene above we have a thousand particles in continous motion. Whenever a particle collides with another, their color changes to black. However, this is a large number of particles with a pairwise comparison algorithm (double for loop) checking if collisions are occuring. This results in a O(n^2) time complexity, causing the number of n checks to increase quadratically which is pretty terrible and you can see that from the fps counter. Now Imagine if we're doing the same collision check in a 3D world consisting of thousands of objects with textures and shaders. This is where a quad tree comes into play.

After creating a quad tree for the same scene and inserting every particle inside of it you can see that the we got a signficant performance boost. By using the query function, we loop through all the points within our scene and pass them to our function. We then obtain the points that are stored in the same node the passed point is or in other words the points that have a high chance of colliding with our passed point and return it for starting our collision checks. That way we reduced our checks from 1000^2 checks to a reduced number that depends on how many objects a single node can store. Let's take a look on how to implement the query function.

And that's it! That's how to implement a fully functional quad tree for spatial partitioning. I should note that there are various other quad tree applications not limited to improving performance for collision checks. Some common uses of the quad tree data structure are image processing, image representation and mesh generation a topic I will most probably write a tutorial for in the near future. For now try to implement the quad tree yourself!